こんにちはー、かけるです!
前回、【C言語】ビットボードを使ったリバーシプログラムを作ってみたの記事で、筆者が作ったリバーシプログラムを公開させていただきました。
――で、せっかくリバーシプログラムを作るなら、そのAIも誰しも少しくらいは強いものにしたいと思うはず。
筆者自身、今も気が向いたときにAIの探索を練り直したりしています。そこで、今回はAIを実装するための足がけとして、探索アルゴリズムについて簡単に整理してみました。
探索アルゴリズムとは
探索アルゴリズムとは、数多ある選択肢の中からとある条件を満たすものを見つけ出すための考え方のことです。つまり、これを今回のケースに置き換えるのであれば、リバーシで勝つために最も有効となる一手を先読みするための考え方ということになります。
この記事では、リバーシや将棋のようなゲームでの探索アルゴリズムを語る上ですべての基本となる「ミニマックス法」「アルファベータ法」について紹介します。
ミニマックス(Mini-Max)法
ミニマックス法とは
ミニマックス法とは、お互いのプレイヤーが自身にとって最も最善な手を選ぶと仮定して探索する手法です。具体的な探索内容は、以下の図をもとに解説します。

はじめに、こういった最善手の探索を必要としているのは大抵がAI側であるため、現在の盤面=AI側のターンであることを前提に解説を進めます。
AI側は現在の局面に対し、AとHの2か所に石を置くことができる状況とします。ここでは1手目でAに置いたと仮定して次の局面を考えます。AIが石を置いた次はPlayerの手番であり、Playerも同じように石を置ける場所の中から1箇所を選んで石を置くため、ここではBの位置に置いたと仮定しましょう。
対局が順当に進んでいれば次は再びAIの手番であり、AIはCとDの位置に石を置くことができます。この図の例ではC、Dは探索の終端であるため、Cに置いたとき、Dに置いたときそれぞれの局面に対し、優劣をつけるための評価を行います。
図の例ではCの局面が6点、Dの局面が8点であり、3手目は自身(AI)の手番であるため、この中で最も高い評価値(この場合はDの8点)がBの評価値となります。
Eの局面の評価値も、Bと同じように考えると9点が与えられることがわかります。これで2手目B、Eそれぞれの局面の評価値が決まったので、Aの評価値を考えることができるようになります。では、Aの評価値もB、Eの中から最も高い評価値で良いのでしょうか?
これはNoです。何故なら、AIから見て対戦相手であるPlayerも同じように勝利を目指しているため、自身(AI)にとって不利となる手を打ってくると考えられます。したがって、対戦相手が手番のときは最も低い評価値(この場合はBの8点)がAの評価値となります。
Aの評価値が確定したら、次にHの評価値も同じ手順で調べます(図では6点となる)。
最後にAとHの評価値はAの方が高いため、AIにとっての最善な手はAであることがわかります。
ミニマックス法の利点
ミニマックス法を使う一番の利点として、評価内容に沿った確実な結果を得られる点が挙げられます。ものすごく極端な例ですが、60手読み、石の数による評価でミニマックス法を使って探索した場合、必勝パターンの探索も事実上は可能ということです。
ミニマックス法の欠点
ミニマックス法を使用する上での欠点としては、考えられるすべての局面を探索するため探索数がとにかく膨大となってしまう点が挙げられます。
その欠点がどれほどのものか調べた結果を以下に示します。
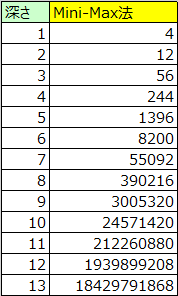
上記はAIが先攻1手目で探索した場合の局面数を表しています。
13手読みした場合の局面数でさえ約184億であり、14手読み以降も1手深くなるごと数が膨大化していく様子がわかると思います。故に事実上は可能と言った必勝パターンの探索も現実的には不可能といっても過言ではありません。しかし、この欠点を改善した探索の手法として、アルファベータ法といった手法があります。
アルファベータ(Alpha-Beta)法
アルファベータ法とは
アルファベータ法も基本的には前述のミニマックス法と同じような探索ですが、こちらは探索結果に影響しない部分について枝刈りを行うことで探索数の削減を図った手法です。ミニマックス法との具体的な差異は以下の図をもとに解説します。

はじめにミニマックス法のときと同じくCとDの評価値を調べ、Bの評価値(8点)を確定させます。ここまではミニマックス法と全く同じです。次にEの評価値を調べるためにFの局面を調べますが、ここからミニマックス法とのアルファベータ法で探索にちがいが出てきます。
まずはFの評価値(9点)を調べます。この時点でGの評価値は不明ですが、Eの評価値はFとGの評価値のうち最も高い値に決まるため、少なくともEの評価値が9点以上になることはわかります。
また、対戦相手(Player)はBとEのうち、AIにとって最も評価値が低くなる手を選択します。つまり、すでにBは8点、Eが9点以上とわかっているため、Eの手が選ばれることはないことがわかります。よって、Gの評価値を調べる必要がないことになります。
このように、探索結果に影響しないことがわかった時点で探索を打ち切ることで、ミニマックス法で欠点としていた探索数の削減を図っています。
アルファベータ法による改善効果
アルファベータ法による改善効果のほどを以下に示します。
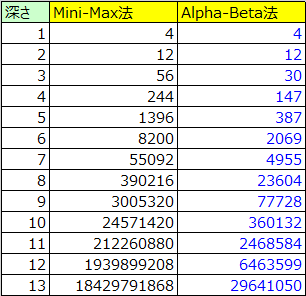
上記もミニマックス法のときと同じく、AIが先攻1手目で探索した場合の局面数を表しています。
アルファベータ法を使用することで、13手先読み時の局面数が約184億⇒約3000万と大きく削減に成功していることがわかります。とは言え、必勝パターンの探索はこれでも現実的に不可能だろうことは変わりませんが・・・。
また、ミニマックス法との変化点は探索が不要とわかった枝のみを枝刈りしているため、探索で得られる結果はミニマックス法と変わりません。
<2021.03.28追記>上記の結果を微量ですが、さらに改善したものを【リバーシプログラム】Alpha-Beta法の改善案のページにまとめたので、こちらもご参照ください。
以上、最後まで読んでいただきありがとうございます!それでは、また(・ω・)ノシ


コメント